평면의 벡터 방정식

앞서 알아보았던 직선의 벡터 방정식처럼 평면의 벡터 방정식에 대해서도 알아본다.

 

 

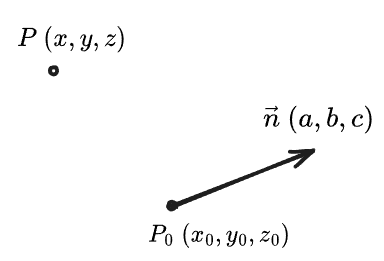
위 사진처럼 값을 알고 있는 점 P0와, normal 벡터 n이 있을 때, 벡터 n과 수직 관계인 모든 점들을 모아보자.

그럼 아래의 사진처럼 점들은 어떤 평면 위에 위치함을 생각해볼 수 있으며, 그 중 어떤 한 점을 P라고 하자.

 

 

수직 관계인 두 벡터의 내적은 0이므로, 이를 이용하기 위해 어떤 점 P를 향하는 벡터를 구하면 다음과 같다.

 

 

 

따라서, 다음과 같이 어떤 점 P를 사용하여 표현된 평면의 벡터 방정식을 얻을 수 있다.

 

 

 

이 식에서 중요한 점은 두 벡터 n과 p의 관계가 수직이어야 성립된다는 점이다.

또한, 위의 식을 통해 벡터가 아닌 평면의 (스칼라) 방정식을 도출할 수도 있다.

 

벡터를 각각의 축 성분에 대해 풀어서 내적을 계산해보면 다음과 같다.

 

 

 

위의 식을 다시 각각의 x, y, z축 성분에 대해서 정리한다.

 

 

 

여기서 상수항 전체를 d로 치환하면 아래와 같이 깔끔한 식이 도출된다.

 

 

 

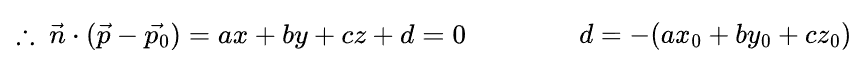
이 식에서 각 축의 성분이 벡터 n (normal vector)의 성분과 같으며,

벡터 n이 정규화된 상태면 상수항 d는 원점과 평면 사이의 수직 거리를 의미한다.

    > 정규화되지 않았다면 d를 벡터 n의 크기로 나눠주면 된다.

---

 

Reference

• https://mathjk.tistory.com/4208
• https://www.songho.ca/math/plane/plane.html