AABB (Axis Aligned Bounding Box) 충돌 감지

간단히 말해보자면 직각좌표계의 각 축에 정렬된 (평행한) 사각형 (Bounding Box 혹은 Collision Box) 에 대해서, 그 사각형의 최소/최대 좌표값을 이용하여 충돌을 판단한다.

 

 

먼저, x축 상에서 사각형을 형성하는 각각의 두 점의 x축 값을 이용하여 충돌이 되었는지 검사한다.

이 경우 두 사각형은 좌측, 우측에서 충돌하는 (겹쳐지는) 총 두 가지 case가 생길 수 있다.

 

여기서 겹쳐진다는 것은 각 축에 투영된 부분이 겹치는 경우이며, 한 축당 두 가지 경우에 대한 검사를 필요로 한다.

따라서, 한 축에 두 가지 경우에 대한 검사가 필요하고 아래 부등식을 모두 만족한다면 충돌했다고 할 수 있다.

 

 

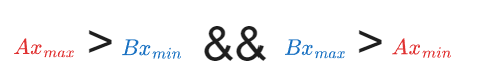
그리고, 축을 하나 늘려 위와 동일한 방식으로 y축 상에서 충돌 되었는지 검사한다.

 

 

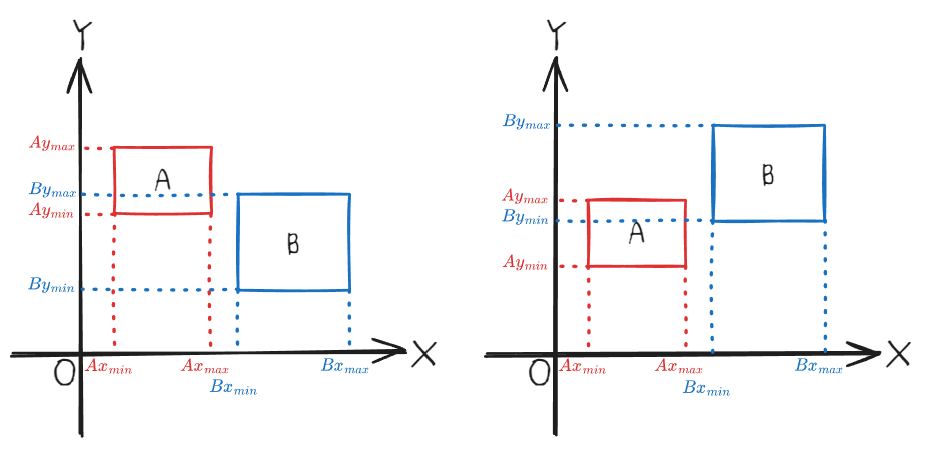
결론적으로, x축과 y축에 대해서 검사하고 총 네 가지 부등식을 모두 통과하는 경우 두 객체는 충돌했다고 판단한다.

 

 

 

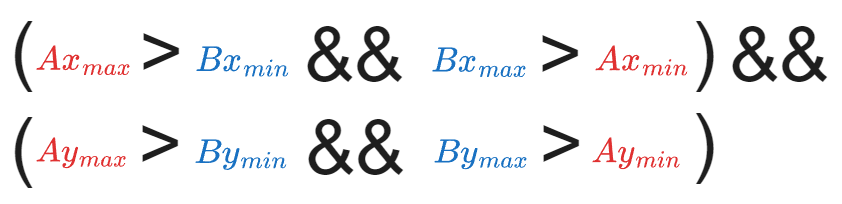
AABB 방식의 단점으로는 객체가 회전하더라도 Bounding Box 자체는 회전하지 않는다. (Axis-Aligned)

그래서 정밀한 검사가 불가능하지만 간단해서 빠르다는 장점이 있다.

 

마지막으로 아래 예제를 통해 충돌하지 않은 경우와 충돌한 경우에 대해 알아본다.

 

 

 

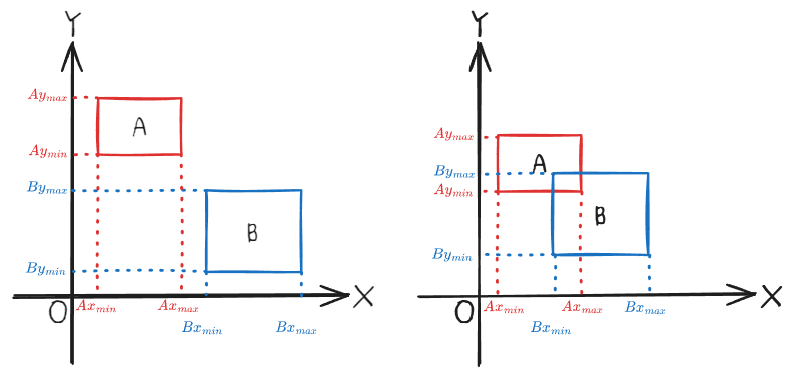
좌측의 겹쳐있지 않은 경우를 먼저 예로 들어보자면 y축에 대한 검사 중 마지막 검사에서 성립하지 않는다.

우측의 겹쳐진 경우에는 모든 검사에 대해 통과하기 때문에 충돌했다고 판단한다.

 

만약 3차원에서 검사를 수행하고 싶다면, z축에 대한 검사가 추가된 부등식을 사용하면 된다.

 

bool isColliding(const CollisionBox& cb1, const CollisionBox& cb2) {
    bool xColliding = ((cb1.xMax > cb2.xMin) && (cb2.xMax > cb1.xMin));
    bool yColliding = ((cb1.yMax > cb2.yMin) && (cb2.yMax > cb1.yMin));
    bool zColliding = ((cb1.zMax > cb2.zMin) && (cb2.zMax > cb1.zMin));
    
    return (xColliding && yColliding && zColliding);
}

---

Reference

• https://learnopengl.com/In-Practice/2D-Game/Collisions/Collision-detection